El algoritmo para calcular la raíz cúbica a mano es idéntico al de la raíz cuadrada salvo las diferencias en la expansión binomial  respecto a
respecto a 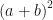 .
.
En el algoritmo de raíz cuadrada, se usa la expansión  de tal forma que al separar los digitos de
de tal forma que al separar los digitos de 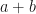 en pares podamos aproximar el primer numero
en pares podamos aproximar el primer numero  dejando el resto de la expresión para repeticiones sucesivas del algoritmo. De este modo cuando en el siguiente paso hacemos «el doble del numero que elegimos agregando otro tal que multiplicado por el numero que agregamos sea menor que el resto dentro de la casita» es exactamente lo mismo que hacer
dejando el resto de la expresión para repeticiones sucesivas del algoritmo. De este modo cuando en el siguiente paso hacemos «el doble del numero que elegimos agregando otro tal que multiplicado por el numero que agregamos sea menor que el resto dentro de la casita» es exactamente lo mismo que hacer  que es el complemento de la expansión binomial (con la ligera diferencia de que $a$ es un multiplo de 10). Para la raíz cúbica se hará lo mismo en cada paso, entonces:
que es el complemento de la expansión binomial (con la ligera diferencia de que $a$ es un multiplo de 10). Para la raíz cúbica se hará lo mismo en cada paso, entonces:
ALGORITMO
1.- Separamos los digitos de 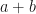 en ternas de derecha a izquierda a partir del punto decimal y después del punto, de izquierda a derecha.
en ternas de derecha a izquierda a partir del punto decimal y después del punto, de izquierda a derecha.
2.- Se aproxima por abajo la raíz cúbica del numero (en bloques de comas) más a la izquierda y se anota en el resultado calculando el resto y agregando la siguiente terna.
3.- Usando el resultado actual multiplicado por 10 como  y agregando un
y agregando un 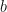 de tal forma que la expresión
de tal forma que la expresión 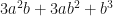 aproxime por abajo al resto actual. Calculamos el resto, agregamos la siguiente terna (si la hay).
aproxime por abajo al resto actual. Calculamos el resto, agregamos la siguiente terna (si la hay).
4.- Se repite el paso 3 hasta terminar con las ternas o hasta la precisión deseada.
EJEMPLO ![\sqrt[3]{15363967256}=2486](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B15363967256%7D%3D2486&bg=ffffff&fg=111111&s=0&c=20201002)
Paso 1: Separamos los digitos en ternas.
![\sqrt[3]{15,363,967,256}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B15%2C363%2C967%2C256%7D&bg=ffffff&fg=111111&s=0&c=20201002)
Paso 2: Aproximamos ![\sqrt[3]{15}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B15%7D&bg=ffffff&fg=111111&s=0&c=20201002) por debajo, esto es 2. De modo que
por debajo, esto es 2. De modo que  , lo anotamos y agregamos la siguiente terna de arriba 363.
, lo anotamos y agregamos la siguiente terna de arriba 363.
![\begin{array}{ll}\sqrt[3]{15,363,967,256} & 2 \\\text{ \ \ \ }7,363 &\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5Csqrt%5B3%5D%7B15%2C363%2C967%2C256%7D+%26+2+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%7D7%2C363+%26%5Cend%7Barray%7D&bg=ffffff&fg=111111&s=0&c=20201002)
Paso 3: Hacemos  y pensamos un
y pensamos un 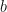 tal que
tal que  . Reexpresando tenemos:
. Reexpresando tenemos: 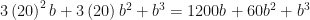 , donde el termino «lider» es
, donde el termino «lider» es  seleccionando b=4 obtenemos
seleccionando b=4 obtenemos  . Anotamos el 4 (el valor de
. Anotamos el 4 (el valor de 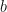 que elegimos), calculamos el resto 7363-5824=1539, lo anotamos debajo y bajamos la siguiente terna. (Note que con b=5 nos hubieramos pasado del resto obteniendo
que elegimos), calculamos el resto 7363-5824=1539, lo anotamos debajo y bajamos la siguiente terna. (Note que con b=5 nos hubieramos pasado del resto obteniendo  ).
).
![\begin{array}{ll}\sqrt[3]{15,363,967,256} & 24 \\\text{ \ \ \ }7,363 & 3\left( 20\right) ^{2}\left( 4\right) +3\left(20\right) \left( 4\right) ^{2}+\left( 4\right) ^{3}=\allowbreak 5,824 \\\text{ \ \ \ }1,539,967 &\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5Csqrt%5B3%5D%7B15%2C363%2C967%2C256%7D+%26+24+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%7D7%2C363+%26+3%5Cleft%28+20%5Cright%29+%5E%7B2%7D%5Cleft%28+4%5Cright%29+%2B3%5Cleft%2820%5Cright%29+%5Cleft%28+4%5Cright%29+%5E%7B2%7D%2B%5Cleft%28+4%5Cright%29+%5E%7B3%7D%3D%5Callowbreak+5%2C824+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%7D1%2C539%2C967+%26%5Cend%7Barray%7D&bg=ffffff&fg=111111&s=0&c=20201002)
Paso 3 (Segunda iteración): Ahora hacemos 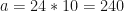 y pensamos un
y pensamos un 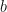 tal que
tal que  . Reexpresando:
. Reexpresando:  , donde el termino «lider» es
, donde el termino «lider» es  seleccionando b=8 obtenemos
seleccionando b=8 obtenemos  . Anotamos el 8 (el valor de
. Anotamos el 8 (el valor de 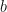 que elegimos), calculamos el resto 1,539,967-1,428,992=110,975, lo anotamos debajo y bajamos la siguiente terna.
que elegimos), calculamos el resto 1,539,967-1,428,992=110,975, lo anotamos debajo y bajamos la siguiente terna.
![\begin{array}{ll}\sqrt[3]{15,363,967,256} & 248 \\\text{ \ \ \ }7,363 & 3\left( 20\right) ^{2}\left( 4\right) +3\left(20\right) \left( 4\right) ^{2}+\left( 4\right) ^{3}=\allowbreak 5,824 \\\text{ \ \ \ }1,539,967 & 3\left( 240\right) ^{2}\left( 8\right) +3\left(240\right) \left( 8\right) ^{2}+\left( 8\right) ^{3}=1,428\,,992 \\\text{ \ \ \ \ \ \ }110,975,256 &\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5Csqrt%5B3%5D%7B15%2C363%2C967%2C256%7D+%26+248+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%7D7%2C363+%26+3%5Cleft%28+20%5Cright%29+%5E%7B2%7D%5Cleft%28+4%5Cright%29+%2B3%5Cleft%2820%5Cright%29+%5Cleft%28+4%5Cright%29+%5E%7B2%7D%2B%5Cleft%28+4%5Cright%29+%5E%7B3%7D%3D%5Callowbreak+5%2C824+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%7D1%2C539%2C967+%26+3%5Cleft%28+240%5Cright%29+%5E%7B2%7D%5Cleft%28+8%5Cright%29+%2B3%5Cleft%28240%5Cright%29+%5Cleft%28+8%5Cright%29+%5E%7B2%7D%2B%5Cleft%28+8%5Cright%29+%5E%7B3%7D%3D1%2C428%5C%2C%2C992+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%5C+%5C+%5C+%7D110%2C975%2C256+%26%5Cend%7Barray%7D&bg=ffffff&fg=111111&s=0&c=20201002)
Paso 3 (Tercera iteración): Ahora hacemos  y pensamos un
y pensamos un 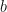 tal que
tal que  . Reexpresando tenemos:
. Reexpresando tenemos: 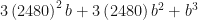 , donde el termino «lider» es
, donde el termino «lider» es  seleccionando b=6 obtenemos
seleccionando b=6 obtenemos 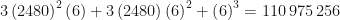 . Anotamos el 6 (el valor de $b$ que elegimos), calculamos el resto 110,975,256-11,097,256=0, lo anotamos debajo y como el resto es cero, la raíz es exacta.
. Anotamos el 6 (el valor de $b$ que elegimos), calculamos el resto 110,975,256-11,097,256=0, lo anotamos debajo y como el resto es cero, la raíz es exacta.
![\begin{array}{ll}\sqrt[3]{15,363,967,256} & 2486 \\\text{ \ \ \ }7,363 & 3\left( 20\right) ^{2}\left( 4\right) +3\left(20\right) \left( 4\right) ^{2}+\left( 4\right) ^{3}=\allowbreak 5,824 \\\text{ \ \ \ }1,539,967 & 3\left( 240\right) ^{2}\left( 8\right) +3\left(240\right) \left( 8\right) ^{2}+\left( 8\right) ^{3}=1,428\,,992 \\\text{ \ \ \ \ \ \ }110,975,256 & 3\left( 2480\right) ^{2}\left( 6\right)+3\left( 2480\right) \left( 6\right) ^{2}+\left( 6\right) ^{3}=\allowbreak 110\,975\,256 \\\text{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }0 &\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5Csqrt%5B3%5D%7B15%2C363%2C967%2C256%7D+%26+2486+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%7D7%2C363+%26+3%5Cleft%28+20%5Cright%29+%5E%7B2%7D%5Cleft%28+4%5Cright%29+%2B3%5Cleft%2820%5Cright%29+%5Cleft%28+4%5Cright%29+%5E%7B2%7D%2B%5Cleft%28+4%5Cright%29+%5E%7B3%7D%3D%5Callowbreak+5%2C824+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%7D1%2C539%2C967+%26+3%5Cleft%28+240%5Cright%29+%5E%7B2%7D%5Cleft%28+8%5Cright%29+%2B3%5Cleft%28240%5Cright%29+%5Cleft%28+8%5Cright%29+%5E%7B2%7D%2B%5Cleft%28+8%5Cright%29+%5E%7B3%7D%3D1%2C428%5C%2C%2C992+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%5C+%5C+%5C+%7D110%2C975%2C256+%26+3%5Cleft%28+2480%5Cright%29+%5E%7B2%7D%5Cleft%28+6%5Cright%29%2B3%5Cleft%28+2480%5Cright%29+%5Cleft%28+6%5Cright%29+%5E%7B2%7D%2B%5Cleft%28+6%5Cright%29+%5E%7B3%7D%3D%5Callowbreak+110%5C%2C975%5C%2C256+%5C%5C%5Ctext%7B+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%7D0+%26%5Cend%7Barray%7D&bg=ffffff&fg=111111&s=0&c=20201002)
De este modo:
![\sqrt[3]{15,363,967,256}=2486](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B15%2C363%2C967%2C256%7D%3D2486&bg=ffffff&fg=111111&s=0&c=20201002)
Como este procedimiento es general, para cualquier entero  basta con sustituir las referencias cúbicas por n-ésimas y la expansión binomial cúbica por la n-ésima
basta con sustituir las referencias cúbicas por n-ésimas y la expansión binomial cúbica por la n-ésima  .
.
Post #01 – mycomplexsoul
de
parámetros a un conjunto de
datos
, definimos
con
y
no lineal con
cómo i-ésima componente.
es una función semi-paraboidal en el sentido de que es la suma de parábolas y por tanto es minimizable.
tal que
se minimiza, hallamos las soluciones del gradiente de
de este modo, definiendo
como el jacobiano de
tenemos las 2 primeras derivadas de
:
tenemos:
a los siguientes datos:
entonces:
y 8 decimales tenemos:
la cual se ajusta a los datos.