Autor: mycomplexsoul

El problema del Cumpleaños

Posted by

0

¿Cuántas personas necesitamos reunir para que dos de ellas coincidan en el día de su cumpleaños con una probabilidad mayor del 50%?

También conocido como «La Paradoja del Cumpleaños», este problema va en contra de la intuición normal al ser un número realmente «pequeño» el que se requiere para dar respuesta a la pregunta.

El problema ha sido ampliamente desarrollado en Internet, por lo que quizá lo mejor es recopilar algunas referencias completas sobre la solución del mismo:

+ [Wikipedia.org] Paradoja del Cumpleaños

+ [EstadísticaParaTodos.es] La Paradoja del Cumpleaños

+ [Gaussianos.com] La Paradoja del Cumpleaños

* Para los que buscan la solución rápida: 23 personas con probabilidad mayor a 50.7%.

Post #13 – mycomplexsoul

La Identidad de Pascal

Posted by

0

Sean n y r enteros positivos con r\leq n. Entonces

\binom{n}{r}=\binom{n-1}{r-1}+\binom{n-1}{r}

DEMOSTRACIÓN

La demostración se realiza de forma algebraica mostrando que el lado derecho es reducible al lado izquierdo.

\binom{n-1}{r-1}+\binom{n-1}{r}=\frac{\left( n-1\right) !}{\left( r-1\right) !\left( n-r\right) !}+\frac{\left( n-1\right) !}{r!\left(n-r-1\right) !}

Multiplicando por la identidad convenientemente, el primer término por \frac{r}{r} y el segundo por \frac{n-r}{n-r}

=\frac{r\left( n-1\right) !}{r\left( r-1\right) !\left( n-r\right) !}+\frac{\left( n-r\right) \left( n-1\right) !}{r!\left( n-r\right) \left(n-r-1\right) !}

Completando factoriales

=\frac{r\left( n-1\right) !}{r!\left( n-r\right) !}+\frac{\left( n-r\right)\left( n-1\right) !}{r!\left( n-r\right) !}

Factorizando el término común

=\frac{\left( n-1\right) !}{r!\left( n-r\right) !}\left( r+\left(n-r\right) \right)

Simplificando

=\frac{\left( n-1\right) !n}{r!\left( n-r\right) !}

Completando factorial

=\frac{n!}{r!\left( n-r\right) !}

=\binom{n}{r}

Así la identidad queda demostrada.

Post #12 – mycomplexsoul

Linealizar Potencias Enteras De Coseno

Posted by

0

La expresión general 2^{n}\cos ^{n}\left( x\right) que es una potencia de la función trigonométrica coseno, es reducible a una suma de cosenos lineales de acuerdo a la siguiente fórmula.

Proposición:

2^{n}\cos ^{n}\left( x\right) =\left\{ \begin{array}{cc} \sum\limits_{i=0}^{\left\lceil \frac{n-1}{2}\right\rceil }\binom{n}{i}2\cos\left( \left( n-2i\right) x\right) & n\text{ impar} \\ \sum\limits_{i=0}^{\left\lceil \frac{n-1}{2}\right\rceil -1}\binom{n}{i} 2\cos \left( \left( n-2i\right) x\right) +2\binom{n-1}{\left\lceil \frac{n-1}{2}\right\rceil -1} & n\text{ par} \end{array} \right.

La demostración se hará por inducción para n par e impar, demostrando pares e impares por separado.

DEMOSTRACIÓN

Con n impar

Para n=1 tenemos:

2^{1}\cos ^{1}\left( x\right) =\sum\limits_{i=0}^{\left\lceil \frac{1-1}{2}\right\rceil }\binom{1}{i}2\cos \left( \left( 1-2i\right) x\right) =2\cos \left( x\right)

Suponemos para n=2p-1

2^{2p-1}\cos ^{2p-1}\left( x\right) =\sum\limits_{i=0}^{p-1}\binom{2p-1}{i}2\cos \left( \left( 2p-1-2i\right) x\right)

Para demostrar el siguiente impar multiplicamos por 2^{2}\cos ^{2}\left( x\right)

\left( 2^{2}\cos ^{2}\left( x\right) \right) \left( 2^{2p-1}\cos ^{2p-1}\left( x\right) \right) =\left( 2^{2}\cos ^{2}\left( x\right) \right) \sum\limits_{i=0}^{p-1}\binom{2p-1}{i}2\cos \left( \left( 2p-1-2i\right) x\right)

Introduciendo a la sumatoria y viendo que 2^{2}\cos ^{2}\left( x\right) =2\left( \cos 2x+1\right)

=\sum\limits_{i=0}^{p-1}\binom{2p-1}{i}2\left( \cos \left( \left( 2p-1-2i\right) x\right) \left( 2\left( \cos 2x+1\right) \right) \right)

Multiplicando

=\sum\limits_{i=0}^{p-1}\binom{2p-1}{i}2\left( 2\cos \left( \left( 2p-1-2i\right) x\right) \left( \cos 2x\right) +2\cos \left( \left( 2p-1-2i\right) x\right) \right)

Utilizando la identidad trigonométrica 2\cos x\cos y=\cos \left( x+y\right) +\cos \left( x-y\right)

=\sum\limits_{i=0}^{p-1}\binom{2p-1}{i}2\left( \cos \left( \left( 2p-1-2i+2\right) x\right) +\cos \left( \left( 2p-1-2i-2\right) x\right) +2\cos \left( \left( 2p-1-2i\right) x\right) \right)

Separando sumatorias

=\sum\limits_{i=0}^{p-1}\binom{2p-1}{i}2\cos \left( \left( 2p-1-2i+2\right) x\right) +\sum\limits_{i=0}^{p-1}\binom{2p-1}{i}2\cos \left( \left(2p-1-2i-2\right) x\right) +\sum\limits_{i=0}^{p-1}\binom{2p-1}{i}2^{2}\cos\left( \left( 2p-1-2i\right) x\right)

Para poder sumar correctamente vamos a separar los dos primeros terminos de la primera sumatoria, los dos últimos terminos de la segunda sumatoria, el primero y el último termino de la tercera sumatoria. De este modo:

=\sum\limits_{i=2}^{p-1}\binom{2p-1}{i}2\cos \left( \left( 2p-1-2i+2\right) x\right) +\sum\limits_{i=0}^{p-3}\binom{2p-1}{i}2\cos \left( \left( 2p-1-2i-2\right) x\right) +\sum\limits_{i=1}^{p-2}\binom{2p-1}{i}2^{2}\cos \left( \left( 2p-1-2i\right) x\right)

+\binom{2p-1}{0}2\cos \left( \left( 2p+1\right) x\right) +\binom{2p-1}{1}2\cos \left( \left( 2p-1\right) x\right) +\binom{2p-1}{p-2}2\cos \left( \left( 1\right) x\right) +\binom{2p-1}{p-1}2\cos \left( \left( -1\right) x\right)

+\binom{2p-1}{0}2^{2}\cos \left( \left( 2p-1\right) x\right) +\binom{2p-1}{p-1}2^{2}\cos \left( \left( 1\right) x\right)

Ahora simplemente renombramos y en los terminos separados sumamos recordando que \cos x=\cos \left( -x\right)

=\sum\limits_{j=0}^{p-3}\binom{2p-1}{j+2}2\cos \left( \left( 2p-3-2j\right) x\right) +\sum\limits_{j=0}^{p-3}\binom{2p-1}{j}2\cos \left( \left( 2p-3-2j\right) x\right) +\sum\limits_{j=0}^{p-3}\binom{2p-1}{j+1}2^{2}\cos \left( \left( 2p-3-2j\right) x\right)

+\binom{2p-1}{0}2\cos \left( \left( 2p+1\right) x\right) +\left( \binom{2p-1}{1}+2\binom{2p-1}{0}\right) 2\cos \left( \left( 2p-1\right) x\right) +\left( \binom{2p-1}{p-2}+\binom{2p-1}{p-1}+2\binom{2p-1}{p-1}\right) 2\cos \left( \left( 1\right) x\right)

Factorizando

=\sum\limits_{j=0}^{p-3}\left( \binom{2p-1}{j+2}+\binom{2p-1}{j}+2\binom{2p-1}{j+1}\right) 2\cos \left( \left( 2p-3-2j\right) x\right)

+\binom{2p-1}{0}2\cos \left( \left( 2p+1\right) x\right) +\left( 2p-1+2\left( 1\right) \right) 2\cos \left( \left( 2p-1\right) x\right) +\left( \frac{\left( 2p-1\right) !}{\left( p-2\right) !\left( p+1\right) !}+3\frac{\left( 2p-1\right) !}{\left( p-1\right) !p!}\right) 2\cos \left( \left( 1\right) x\right)

Reexpresando convenientemente

=\sum\limits_{j=0}^{p-3}\left( \frac{\left( 2p-1\right) !}{\left( j+2\right) !\left( 2p-3-j\right) !}+\frac{\left( 2p-1\right) !}{j!\left( 2p-1-j\right) !}+2\frac{\left( 2p-1\right) !}{\left( j+1\right) !\left( 2p-2-j\right) !}\right) 2\cos \left( \left( 2p-3-2j\right) x\right)

+\binom{2p-1}{0}2\cos \left( \left( 2p+1\right) x\right) +\left( 2p+1\right) 2\cos \left( \left( 2p-1\right) x\right) +\left( 2p-1\right) !\left( \frac{1}{\left( p-2\right) !\left( p+1\right) !}+3\frac{1}{\left( p-1\right) !p!}\right) 2\cos \left( \left( 1\right) x\right)

=\sum\limits_{j=0}^{p-3}\frac{\left( 2p-1\right) !}{j!\left( 2p-1-j\right) !}\left( \frac{\left( 2p-1-j\right) \left( 2p-2-j\right) }{\left( j+2\right) \left( j+1\right) }+1+2\frac{\left( 2p-1-j\right) }{\left( j+1\right) }\right) 2\cos \left( \left( 2p-3-2j\right) x\right)

+\binom{2p-1}{0}2\cos \left( \left( 2p+1\right) x\right) +\left( 2p+1\right) 2\cos \left( \left( 2p-1\right) x\right) +\frac{\left( 2p-1\right) !}{p!\left( p-1\right) !}\left( \frac{\left( p-1\right) }{\left( p+1\right) }+3\right) 2\cos \left( \left( 1\right) x\right)

Sumando

=\sum\limits_{j=0}^{p-3}\frac{\left( 2p-1\right) !}{j!\left( 2p-1-j\right) !}\left( \frac{\left( 2p\right) \left( 2p+1\right) }{\left( j+2\right) \left( j+1\right) }\right) 2\cos \left( \left( 2p-3-2j\right) x\right)

+\binom{2p-1}{0}2\cos \left( \left( 2p+1\right) x\right) +\left( 2p+1\right) 2\cos \left( \left( 2p-1\right) x\right) +\frac{\left( 2p-1\right) !}{p!\left( p-1\right) !}\left( \frac{2\left( 2p+1\right) }{\left( p+1\right) }\right) 2\cos \left( \left( 1\right) x\right)

Reexpresando

=\sum\limits_{j=0}^{p-3}\left( \frac{\left( 2p+1\right) !}{\left( j+2\right) !\left( 2p-1-j\right) !}\right) 2\cos \left( \left( 2p-3-2j\right) x\right)

+\binom{2p-1}{0}2\cos \left( \left( 2p+1\right) x\right) +\left( 2p+1\right) 2\cos \left( \left( 2p-1\right) x\right) +\frac{\left( 2p+1\right) !}{\left( p+1\right) !\left( p-1\right) !}\left( \frac{2}{\left( 2p\right) }\right) 2\cos \left( \left( 1\right) x\right)

Reexpresando convenientemente

=\sum\limits_{j=0}^{p-3}\binom{2p+1}{j+2}2\cos \left( \left( 2p-3-2j\right) x\right) +\binom{2p+1}{0}2\cos \left( \left( 2p+1\right) x\right) +\binom{2p+1}{1}2\cos \left( \left( 2p-1\right) x\right) +\binom{2p+1}{p}2\cos \left( \left( 1\right) x\right)

Reescribiendo el índice de la sumatoria

=\sum\limits_{i=2}^{p-1}\binom{2p+1}{i}2\cos \left( \left( 2p+1-2i\right) x\right) +\binom{2p+1}{0}2\cos \left( \left( 2p+1\right) x\right) +\binom{2p+1}{1}2\cos \left( \left( 2p+1-2\left( 1\right) \right) x\right) +\binom{2p+1}{p}2\cos \left( \left( 2p+1-2\left( p\right) \right) x\right)

Incorporando los terminos separados

=\sum\limits_{i=0}^{p}\binom{2p+1}{i}2\cos \left( \left( 2p+1-2i\right) x\right)

=2^{2p+1}\cos ^{2p+1}\left( x\right)

Demostrado para n impar.

Con n par

Para n=2 tenemos:

2^{2}\cos ^{2}\left( x\right) =\sum\limits_{i=0}^{\left\lceil \frac{2-1}{2}\right\rceil -1}\binom{2}{i}2\cos \left( \left( 2-2i\right) x\right) +2\binom{2-1}{\left\lceil \frac{2-1}{2}\right\rceil -1}=2\cos \left( 2x\right) +2

Suponemos para n=2p

2^{2p}\cos ^{2p}\left( x\right) =\sum\limits_{i=0}^{p-1}\binom{2p}{i}2\cos \left( \left( 2p-2i\right) x\right) +2\binom{2p-1}{p-1}

Para demostrar el siguiente par multiplicamos por 2^{2}\cos ^{2}\left( x\right)

\left( 2^{2}\cos ^{2}\left( x\right) \right) \left( 2^{2p}\cos ^{2p}\left( x\right) \right) =\left( 2^{2}\cos ^{2}\left( x\right) \right) \left( \sum\limits_{i=0}^{p-1}\binom{2p}{i}2\cos \left( \left( 2p-2i\right) x\right) +2\binom{2p-1}{p-1}\right)

Introduciendo a la sumatoria y viendo que 2^{2}\cos ^{2}\left( x\right) =2\left( \cos 2x+1\right)

=\sum\limits_{i=0}^{p-1}\binom{2p}{i}2\left( \cos \left( \left( 2p-2i\right) x\right) \left( 2\left( \cos 2x+1\right) \right) \right) +2 \binom{2p-1}{p-1}\left( 2\cos 2x+2\right)

Multiplicando

=\sum\limits_{i=0}^{p-1}\binom{2p}{i}2\left( 2\cos \left( \left( 2p-2i\right) x\right) \left( \cos 2x\right) +2\cos \left( \left( 2p-2i\right) x\right) \right) +2\binom{2p-1}{p-1}\left( 2\cos 2x+2\right)

Utilizando la identidad trigonométrica 2\cos x\cos y=\cos \left( x+y\right) +\cos \left( x-y\right)

=\sum\limits_{i=0}^{p-1}\binom{2p}{i}2\left( \cos \left( \left( 2p-2i+2\right) x\right) +\cos \left( \left( 2p-2i-2\right) x\right) +2\cos \left( \left( 2p-2i\right) x\right) \right) +2\binom{2p-1}{p-1}\left( 2\cos 2x+2\right)

Separando sumatorias

=\sum\limits_{i=0}^{p-1}\binom{2p}{i}2\cos \left( \left( 2p-2i+2\right) x\right) +\sum\limits_{i=0}^{p-1}\binom{2p}{i}2\cos \left( \left( 2p-2i-2\right) x\right) +\sum\limits_{i=0}^{p-1}\binom{2p}{i}2^{2}\cos \left( \left( 2p-2i\right) x\right) +2\binom{2p-1}{p-1}\left( 2\cos 2x+2\right)

Para poder sumar correctamente vamos a separar los dos primeros terminos de la primera sumatoria, los dos últimos terminos de la segunda sumatoria, el primero y el último termino de la tercera sumatoria. De este modo:

=\sum\limits_{i=2}^{p-1}\binom{2p}{i}2\cos \left( \left( 2p-2i+2\right) x\right) +\sum\limits_{i=0}^{p-3}\binom{2p}{i}2\cos \left( \left( 2p-2i-2\right) x\right) +\sum\limits_{i=1}^{p-2}\binom{2p}{i}2^{2}\cos \left( \left( 2p-2i\right) x\right)

+\binom{2p}{0}2\cos \left( \left( 2p+2\right) x\right) +\binom{2p}{1}2\cos \left( 2px\right) +\binom{2p}{p-2}2\cos \left( 2x\right) +\binom{2p}{p-1}2\cos \left( 0x\right)

+\binom{2p}{0}2^{2}\cos \left( 2px\right) +\binom{2p}{p-1}2^{2}\cos \left( 2x\right) +2\binom{2p-1}{p-1}\left( 2\cos 2x+2\right)

Ahora simplemente renombramos y en los terminos separados sumamos recordando que \cos 0x=1

=\sum\limits_{j=0}^{p-3}\binom{2p}{j+2}2\cos \left( \left( 2p-2-2j\right) x\right) +\sum\limits_{j=0}^{p-3}\binom{2p}{j}2\cos \left( \left( 2p-2-2j\right) x\right) +\sum\limits_{j=0}^{p-3}\binom{2p}{j+1}2^{2}\cos \left( \left( 2p-2-2j\right) x\right)

+\binom{2p}{0}2\cos \left( \left( 2p+2\right) x\right) +\left( \binom{2p}{1}+2\binom{2p}{0}\right) 2\cos \left( 2px\right) +\left( \binom{2p}{p-2}+2\binom{2p}{p-1}+2\binom{2p-1}{p-1}\right) 2\cos \left( 2x\right) +2\binom{2p}{p-1}+2^{2}\binom{2p-1}{p-1}

Factorizando

=\sum\limits_{j=0}^{p-3}\left( \binom{2p}{j+2}+\binom{2p}{j}+2\binom{2p}{j+1}\right) 2\cos \left( \left( 2p-2-2j\right) x\right)

+\binom{2p}{0}2\cos \left( \left( 2p+2\right) x\right) +\left( 2p+2\left( 1\right) \right) 2\cos \left( 2px\right) +\left( \frac{\left( 2p\right) !}{\left( p-2\right) !\left( p+2\right) !}+2\frac{\left( 2p\right) !}{\left( p-1\right) !\left( p+1\right) !}+2\frac{\left( 2p-1\right) !}{\left( p-1\right) !p!}\right) 2\cos \left( 2x\right) +2\left( \frac{\left( 2p\right) !}{\left( p-1\right) !\left( p+1\right) !}+2\frac{\left( 2p-1\right) !}{\left( p-1\right) !p!}\right)

Reexpresando convenientemente

=\sum\limits_{j=0}^{p-3}\left( \frac{\left( 2p\right) !}{\left( j+2\right) !\left( 2p-2-j\right) !}+\frac{\left( 2p\right) !}{j!\left( 2p-j\right) !}+2\frac{\left( 2p\right) !}{\left( j+1\right) !\left( 2p-1-j\right) !}\right) 2\cos \left( \left( 2p-2-2j\right) x\right)

+\binom{2p}{0}2\cos \left( \left( 2p+2\right) x\right) +\left( 2p+2\right) 2\cos \left( 2px\right) +\frac{\left( 2p\right) !}{\left( p-1\right) !\left( p+1\right) !}\left( \frac{\left( p-1\right) }{\left( p+2\right) }+2+2\frac{\left( p+1\right) }{\left( 2p\right) }\right) 2\cos \left( 2x\right) +2\frac{\left( 2p\right) !}{\left( p-1\right) !\left( p+1\right) !}\left( 1+2\frac{\left( p+1\right) }{\left( 2p\right) }\right)

=\sum\limits_{j=0}^{p-3}\frac{\left( 2p\right) !}{j!\left( 2p-j\right) !}\left( \frac{\left( 2p-j\right) \left( 2p-1-j\right) }{\left( j+2\right) \left( j+1\right) }+1+2\frac{\left( 2p-j\right) }{\left( j+1\right) }\right) 2\cos \left( \left( 2p-2-2j\right) x\right)

+\binom{2p}{0}2\cos \left( \left( 2p+2\right) x\right) +\left( 2p+2\right) 2\cos \left( 2px\right) +\frac{\left( 2p\right) !}{\left( p-1\right) !\left( p+1\right) !}\left( \frac{\left( 2p+1\right) \left( 2p+2\right) }{p\left( p+2\right) }\right) 2\cos \left( 2x\right) +2\frac{\left( 2p\right) !}{\left( p-1\right) !\left( p+1\right) !}\left( \frac{2p+1}{p}\right)

Sumando

=\sum\limits_{j=0}^{p-3}\frac{\left( 2p\right) !}{j!\left( 2p-j\right) !}\left( \frac{\left( 2p+1\right) \left( 2p+2\right) }{\left( j+2\right) \left( j+1\right) }\right) 2\cos \left( \left( 2p-2-2j\right) x\right)

+\binom{2p}{0}2\cos \left( \left( 2p+2\right) x\right) +\left( 2p+2\right) 2\cos \left( 2px\right) +\left( \frac{\left( 2p+2\right) !}{p!\left( p+2\right) !}\right) 2\cos \left( 2x\right) +2\left( \frac{\left( 2p+1\right) !}{p!\left( p+1\right) !}\right)

Reexpresando

=\sum\limits_{j=0}^{p-3}\left( \frac{\left( 2p+2\right) !}{\left( j+2\right) !\left( 2p-j\right) !}\right) 2\cos \left( \left( 2p-2-2j\right) x\right)

+\binom{2p}{0}2\cos \left( \left( 2p+2\right) x\right) +\left( 2p+2\right) 2\cos \left( 2px\right) +\left( \frac{\left( 2p+2\right) !}{p!\left( p+2\right) !}\right) 2\cos \left( 2x\right) +2\left( \frac{\left( 2p+1\right) !}{p!\left( p+1\right) !}\right)

Reexpresando convenientemente

=\sum\limits_{j=0}^{p-3}\binom{2p+2}{j+2}2\cos \left( \left( 2p-2-2j\right) x\right) +\binom{2p+2}{0}2\cos \left( \left( 2p+2\right) x\right) +\binom{2p+2}{1}2\cos \left( 2px\right) +\binom{2p+2}{p}2\cos \left( 2x\right) +2\binom{2p+1}{p}

Reescribiendo el índice de la sumatoria

=\sum\limits_{i=2}^{p-1}\binom{2p+2}{i}2\cos \left( \left( 2p+2-2i\right) x\right) +\binom{2p+2}{0}2\cos \left( \left( 2p+2\right) x\right) +\binom{2p+2}{1}2\cos \left( \left( 2p+2-2\left( 1\right) \right) x\right)

+\binom{2p+2}{p}2\cos \left( \left( 2p+2-2\left( p\right) \right) x\right) +2\binom{2p+1}{\left( p+1\right) -1}

Incorporando los terminos separados

=\sum\limits_{i=0}^{p}\binom{2p+2}{i}2\cos \left( \left( 2p+2-2i\right) x\right) +2\binom{2p+1}{\left\lceil \frac{2p+1}{2}\right\rceil -1}

=2^{2p+2}\cos ^{2p+2}\left( x\right)

Demostrado para n par.

Post #11 – mycomplexsoul

Mínimos Cuadrados No Lineales

Posted by

7

Para ajustar un modelo m\left( x,t\right) de n parámetros a un conjunto de m datos \left( t_{i},y_{i}\right) , definimos f\left( x\right) =\frac{1}{2}R\left( x\right) ^{T}R\left( x\right) con R:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m} y R\left( x\right) no lineal con r_{i}\left( x\right) =m\left( x,t_{i}\right) -y_{i} cómo i-ésima componente.

El problema finalmente es:

Minimizar f\left( x\right) =\frac{1}{2}R\left( x\right) ^{T}R\left( x\right) =\frac{1}{2}\sum\limits_{i=1}^{m}r_{i}^{2}\left( x\right)

Esto es equivalente a minimizar la suma de los cuadrados de las diferencias entre el modelo y los datos.

f\left( x\right) es una función semi-paraboidal en el sentido de que es la suma de parábolas y por tanto es minimizable.

Para hallar x tal que f\left( x\right) se minimiza, hallamos las soluciones del gradiente de f\left( x\right) , de este modo, definiendo J\left( x\right) \in \mathbb{R} ^{m\times n} como el jacobiano de R\left( x\right) ,J\left( x\right) _{ij}=\frac{\partial r_{i}\left( x\right) }{\partial x_{j}} tenemos las 2 primeras derivadas de f\left( x\right) :

\nabla f\left( x\right) =\sum\limits_{i=1}^{m}r_{i}\left( x\right) \cdot \nabla r_{i}\left( x\right) =J\left( x\right) ^{T}R\left( x\right)

\nabla ^{2}f\left( x\right) =\sum\limits_{i=1}^{m}\left( \nabla r_{i}\left( x\right) \cdot \nabla r_{i}\left( x\right) ^{T}+r_{i}\left( x\right) \cdot \nabla ^{2}r_{i}\left( x\right) \right) =J\left( x\right) ^{T}J\left( x\right) +S\left( x\right)

Siendo S\left( x\right) =\sum\limits_{i=1}^{m}r_{i}\left( x\right) \cdot \nabla ^{2}r_{i}\left( x\right)

Aplicando el método de Newton para resolver \nabla f\left( x\right) tenemos:

x_{n+1}=x_{n}-\left( \nabla ^{2}f\left( x_{n}\right) \right) ^{-1}\nabla f\left( x_{n}\right)

x_{n+1}=x_{n}-\left( J\left( x_{n}\right) ^{T}J\left( x_{n}\right) +S\left( x_{n}\right) \right) ^{-1}J\left( x_{n}\right) ^{T}R\left( x_{n}\right)

EJEMPLO

Ajustar el modelo y\left( t\right) =e^{tx} a los siguientes datos:

\begin{tabular}{|l|l|l|l|} \hline t & 1 & 2 & 3 \\ \hline y & 2 & 4 & 8 \\ \hline \end{tabular}

De aquí, m\left( x,t_{i}\right) =e^{t_{i}x} entonces:

R=r_{i}\left( x\right) =m\left( x,t_{i}\right) -y_{0}\left( t_{i}\right) =\left( \begin{array}{c} e^{x}-2 \\ e^{2x}-4 \\ e^{3x}-8\end{array}\right)

Ahora f\left( x\right) =\frac{1}{2}R\left( x\right) ^{T}R\left( x\right) =\frac{1}{2}\left[ \left( e^{x}-2\right) ^{2}+\left( e^{2x}-4\right) ^{2}+\left( e^{3x}-8\right) ^{2}\right]

De este modo:

\nabla f\left( x\right) =e^{x}\left( e^{x}-2\right) +2e^{2x}\left( e^{2x}-4\right) +3e^{3x}\left( e^{3x}-8\right)

\nabla ^{2}f\left( x\right) =\left( e^{x}\right) ^{2}+\left( 2e^{2x}\right) ^{2}+\left( 3e^{3x}\right) ^{2}+e^{x}\left( e^{x}-2\right) +4e^{2x}\left( e^{2x}-4\right) +9e^{3x}\left( e^{3x}-8\right)

Finalmente aplicando el método de Newton con:

x_{n+1}=x_{n}-\left( \nabla ^{2}f\left( x_{n}\right) \right) ^{-1}\nabla f\left( x_{n}\right)

Con x_{0}=1 y 8 decimales tenemos:

\begin{tabular}{|l|l|} \hline n & x \\ \hline 0 & 1.00000000 \\ \hline 1 & 0.87299182 \\ \hline 2 & 0.77360001 \\ \hline 3 & 0.71421136 \\ \hline 4 & 0.69491616 \\ \hline 5 & 0.69316064 \\ \hline 6 & 0.69314718 \\ \hline 7 & 0.69314718 \\ \hline \end{tabular}

Obtenemos una convergencia en 7 iteraciones con x_{7}=\ln 2\approx 0.69314718

De modo que y\left( t\right) =e^{t\ln 2}=2^{t} la cual se ajusta a los datos.

Post #10 – mycomplexsoul

Funciones Trigonométricas Hiperbólicas Inversas

Posted by

0

DEFINICIÓN

Las funciones trigonométricas hiperbólicas se definen en términos de la función exponencial de la siguiente manera:

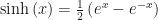
\sinh \left( x\right) =\allowbreak \frac{1}{2}\left( e^{x}-e^{-x}\right)

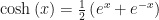
\cosh \left( x\right) =\allowbreak \frac{1}{2}\left( e^{x}+e^{-x}\right)

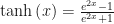
\tanh \left( x\right) =\allowbreak \frac{e^{2x}-1}{e^{2x}+1}

Cuyo dominio es x\in \mathbb{C} (o más estrictamente x\in \mathbb{R}). Y las funciones inversas de éstas se definen en términos de la función logaritmo natural y se pueden deducir despejando las expresiones anteriores, quedando:

\sinh ^{-1}\left( x\right) =\ln \left( x+\sqrt{x^{2}+1}\right)

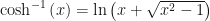
\cosh ^{-1}\left( x\right) =\allowbreak \ln \left( x+\sqrt{x^{2}-1}\right)

\tanh ^{-1}\left( x\right) =\allowbreak \frac{1}{2}\ln \left( \frac{x+1}{1-x}\right)

Cuyo dominio es x\in \mathbb{C} (estrictamente serían x\in \mathbb{R}, x\geq 1, -1<1 respectivamente).

PROBLEMA

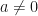No obstante, introducir una simple constante como divisor de x parece oscurecer la forma que debe tener la inversa de la función. Es decir ¿Cuál es la inversa de \sinh \left( \frac{x}{a}\right)? (a\neq 0)

CONJETURANDO

Suponiendo que no conocemos la definición de 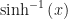\sinh ^{-1}\left( x\right) podemos tratar de hallar la inversa de 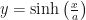y=\sinh \left( \frac{x}{a}\right) mediante la siguiente sucesión de pasos lógicos:

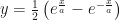
y=\frac{1}{2}\left( e^{\frac{x}{a}}-e^{-\frac{x}{a}}\right)

2y=e^{\frac{x}{a}}-\frac{1}{e^{\frac{x}{a}}}

Como 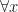e^{\frac{x}{a}}\neq 0 \forall x podemos multiplicar y posteriormente reacomodar

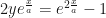
2ye^{\frac{x}{a}}=e^{2\frac{x}{a}}-1

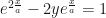
e^{2\frac{x}{a}}-2ye^{\frac{x}{a}}=1

Completando el cuadrado sumando y^{2} a ambos lados y despejando

\left( e^{\frac{x}{a}}-y\right) ^{2}=1+y^{2}

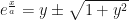
e^{\frac{x}{a}}=y\pm \sqrt{1+y^{2}}

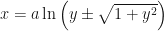
x=a\ln \left( y\pm \sqrt{1+y^{2}}\right)

De este modo la inversa es y=\sinh ^{-1}\left( \frac{x}{a}\right) =a\ln \left( x\pm \sqrt{1+x^{2}}\right) .

CORRIGIENDO EL CAMINO

No obstante esta no es la inversa pues las composiciones \sinh \left( \sinh ^{-1}\left( \frac{x}{a}\right) \right) y \sinh ^{-1}\left( \sinh \left( \frac{x}{a}\right) \right) no coinciden con esta definición. La siguiente igualdad fallará:

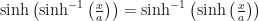
\sinh \left( \sinh ^{-1}\left( \frac{x}{a}\right) \right) =\sinh ^{-1}\left( \sinh \left( \frac{x}{a}\right) \right)

\sinh \left( a\ln \left( x\pm \sqrt{1+x^{2}}\right) \right) =\sinh ^{-1}\left( \frac{1}{2}\left( e^{\frac{x}{a}}-e^{-\frac{x}{a}}\right) \right)

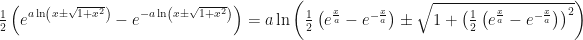
\frac{1}{2}\left( e^{a\ln \left( x\pm \sqrt{1+x^{2}}\right) }-e^{-a\ln \left( x\pm \sqrt{1+x^{2}}\right) }\right) =a\ln \left( \frac{1}{2}\left( e^{\frac{x}{a}}-e^{-\frac{x}{a}}\right) \pm \sqrt{1+\left( \frac{1}{2}\left( e^{\frac{x}{a}}-e^{-\frac{x}{a}}\right) \right) ^{2}}\right)

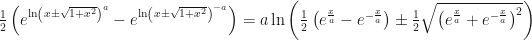
\frac{1}{2}\left( e^{\ln \left( x\pm \sqrt{1+x^{2}}\right) ^{a}}-e^{\ln \left( x\pm \sqrt{1+x^{2}}\right) ^{-a}}\right) =a\ln \left( \frac{1}{2}\left( e^{\frac{x}{a}}-e^{-\frac{x}{a}}\right) \pm \frac{1}{2}\sqrt{\left( e^{\frac{x}{a}}+e^{-\frac{x}{a}}\right) ^{2}}\right)

\frac{1}{2}\left( \left( x\pm \sqrt{1+x^{2}}\right) ^{a}-\left( x\pm \sqrt{1+x^{2}}\right) ^{-a}\right) =a\ln \frac{1}{2}\left( \left( e^{\frac{x}{a}}-e^{-\frac{x}{a}}\right) \pm \left( e^{\frac{x}{a}}+e^{-\frac{x}{a}}\right) \right)

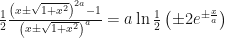
\frac{1}{2}\frac{\left( x\pm \sqrt{1+x^{2}}\right) ^{2a}-1}{\left( x\pm \sqrt{1+x^{2}}\right) ^{a}}=a\ln \frac{1}{2}\left( \pm 2e^{\pm \frac{x}{a}}\right)

Llegado a este paso, el miembro izquierdo de la ecuación no se puede simplificar más a menos que a=1. El lado derecho se simplifica como sigue:

a\ln \frac{1}{2}\left( \pm 2e^{\pm \frac{x}{a}}\right) =a\left( \ln \left( \pm 1\right) +\ln \left( e^{\pm \frac{x}{a}}\right) \right) =a\ln \left( \pm 1\right) \pm x=a\ln \left( 1\right) +x=x

De este modo:

\frac{1}{2}\frac{\left( x\pm \sqrt{1+x^{2}}\right) ^{2a}-1}{\left( x\pm \sqrt{1+x^{2}}\right) ^{a}}=x

El error radica en la forma en que se concibe a la variable independiente en el cálculo de la inversa pues, desde el comienzo se maneja \frac{x}{a} en vez de x de tal forma que podemos interpretar nuestra variable independiente como t=\frac{x}{a}, de este modo el despeje para hallar la inversa es el adecuado:

y=\frac{1}{2}\left( e^{t}-e^{-t}\right)

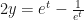
2y=e^{t}-\frac{1}{e^{t}}

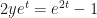
2ye^{t}=e^{2t}-1

e^{2t}-2ye^{t}=1

\left( e^{t}-y\right) ^{2}=1+y^{2}

e^{t}=y\pm \sqrt{1+y^{2}}

t=\ln \left( y\pm \sqrt{1+y^{2}}\right)

De este modo la inversa es y=\sinh ^{-1}\left( \frac{x}{a}\right) =\ln \left( \frac{x}{a}\pm \sqrt{1+\left( \frac{x}{a}\right) ^{2}}\right) .

LA IMPORTANCIA

Es importante tener clara cuál es la función inversa (y su dominio y rango) pues no parece haber referencias fiables siempre a la mano, por ejemplo es muy común que en libros de texto se llegué al cálculo de esta función inversa por medio de una integral, es natural saber cual es la integral a resolver si sabemos que:

\frac{d}{dx}\left( \sinh ^{-1}\left( \frac{x}{a}\right) \right) =\allowbreak \frac{1}{\sqrt{x^{2}+a^{2}}}

De modo que al integrar mediante el cambio de variable x=a\tan \theta obtendremos de forma natural la inversa:

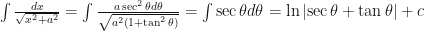
\int \frac{dx}{\sqrt{x^{2}+a^{2}}}=\int \frac{a\sec ^{2}\theta d\theta }{\sqrt{a^{2}\left( 1+\tan ^{2}\theta \right) }}=\int \sec \theta d\theta =\allowbreak \ln \left\vert \sec \theta +\tan \theta \right\vert +c

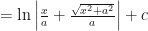
=\ln \left\vert \frac{x}{a}+\frac{\sqrt{x^{2}+a^{2}}}{a}\right\vert +c

Hay muchas referencias textuales que indican que el resultado de la integral (y por lo tanto, la inversa de 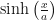\sinh \left( \frac{x}{a}\right) ) es:

\ln \left\vert x+\sqrt{x^{2}+a^{2}}\right\vert +c

Que viene como resultado natural de separar el \ln a y adicionarlo dentro de la constante de integración. Pero esto no es un error dado el contexto de uso, simplemente es un ejercicio de conciencia para la buena manipulación algebraica y conceptual de las funciones trigonométricas hiperbólicas, sobre todo cuando se tienen argumentos con expresiones más elaboradas.

Post #09 – mycomplexsoul